In the physics literature, dimers show up particularly in the study of mirror symmetry as well as statistical mechanics. Dimer models offer an interesting source of balanced quivers (every vertex has in-degree equal to out-degree). Since quivers arising from triangulations are also balanced (with the way we defined them and excluding obvious counterexamples like ideal triangulations on bordered surfaces with punctures), it may be worthwhile studying dimer models to see if there are any interesting properties that arise.
[definition] Let $S$ be a compact oriented Riemann surface. A bipartite tiling $T$ of $S$ is polygonal cell decomposition of $S$ whose nodes and edges form a bipartite graph $\Gamma$. We also define
- $\Gamma_0$ to be the set of nodes of $\Gamma$. Since $\Gamma$ is bipartite, we have $\Gamma_0 = \Gamma_0^\bullet \cup \Gamma_0^\circ$, where we call $\Gamma_0^\bullet$ the black nodes and $\Gamma_0^\circ$
- $\Gamma_1$ to be the set of edges of $\Gamma$
- $\Gamma_2$ to be the set of faces of $\Gamma$ If $\Gamma$ is finite, then we call $\Gamma$ a dimer model. [/definition]
A common approach to an alternative way to realize a dimer $\Gamma$ is to consider its dual oriented using the bipartite property of $\Gamma$ and orientation of the surface. To obtain this oriented dual graph $Q$, we have the following:
- For every face $f$ in $\Gamma$, there is a vertex in $Q$ dual to $f$
- For every edge $e$ in $\Gamma$, there is an edge in $Q$ dual to $e$
- For every node $v$ in $\Gamma$, there is a face in $Q$ dual to $v$ We then orient the faces of $Q$ such that the faces dual to the black nodes of $\Gamma$ are oriented counterclockwise and the faces dual to the white vertices of $\Gamma$ are oriented clockwise.
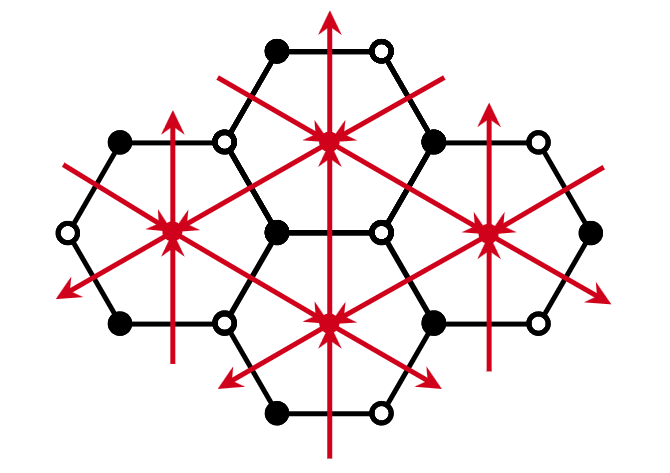
This construction gives a quiver and it is referred to as the dimer quiver. Since there is a sensible notion of clockwise faces and counterclockwise faces due to the bipartiteness of $\Gamma$, we define $Q_2^+$ to be the set of faces oriented counterclockwise and $Q_2^-$ to be the set of faces oriented clockwise.
Recall from the previous post that we defined quiver mutation in a way that requires a quiver to be cluster before we mutate it. A unfortunate(?) consequence of looking at dimer quivers is that it is easy to construct dimers with dimer quivers that are obviously not cluster. Here is an easy example on the sphere:
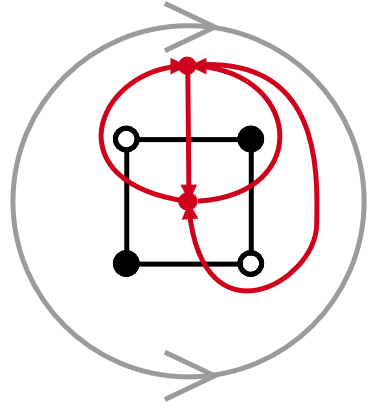
In the above image, there are two counterclockwise cycles and two clockwise cycles. Namely, all four cycles are $2$-cycles so the dimer quiver is not a cluster quiver.
The situation is even worse than the above! By abusing the topology of the surface, we can come up with a dimer where two faces are glued together along more than one edge. This induces a $2$-cycle in the dimer quiver (consider as a purely combinatorial object). This can make it difficult to come up with conditions to define a “reduced” dimer equivalent to a quiver being cluster.
The main issue here is that quiver, considered as purely combinatorial objects, disregard all of the topology involved in the picture. Accordingly, the bandaid we need to define a dimer model version of cluster quivers so we can mutate them is to resort to quivers with potential. In the next post, we will digress to a quick discussion of quivers with potential and then return to a long post on defining the dimer model version of quiver mutation.
Comments