Very forwardly put, quivers are directed multigraphs. One relatively modern interest of quivers is the idea of quiver mutation. There are a lot of good ways to motivate quiver mutation, all of which (to my knowledge, at least) involve cluster algebras in some way or another. The approach we will take is to motivate them through triangulations of a regular $n$-gon (which is rooted in cluster algebra theory, but we will ignore it).
In this post (and for the rest of the sequence of posts on this topic), we will define a triangulation
(of an $n$-gon) as a subdivision of the $n$-gon up into triangles. This subdivision is obtained by taking
the sides of the $n$-gon along with a maximal collection of non-intersecting diagonals (except possibly
at the endpoints). Here is an example of a triangulation of the regular hexagon.
What is not being elaborated upon here, is that we may consider these triangulations in a much more broad and topological context. More generally, one considers a so-called “bordered surface with marked points” and the “ideal triangulations” of these bordered surfaces. This is covered in great detail in the paper Cluster algebras and triangulated surfaces. Part I: Cluster complexes by Fomin, Shapiro, and Thurston. For the sake of simplicity, however, we will just stick to our triangulations of regular $n$-gons.
Something that is of interest in the context of triangulations (at least for our purposes) is the idea of a flip of a diagonal of the triangulation. This is done via the following steps:
- Remove a diagonal from the triangulation
- Observe the “triangulation” now contains a quadrilateral
- Add in the other diagonal of the quadrilateral to the triangulation
- Observe that this gives a new triangulation of the $n$-gon Here’s an example of how two triangulations are related by a single flip of a diagonal:
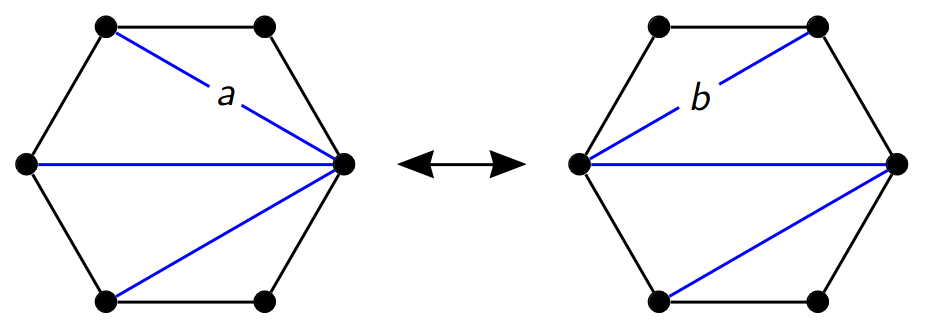
The two triangulations above are related by a flip: To obtain the triangulation on the right, we flip the diagonal labeled $a$ in the triangulation on the left. We can go the other direction to: we flip the diagonal labeled $b$ in the triangulation on the right to obtain the triangulation on the left.
There are many properties that properties that arise out of triangulations. Here are a couple simple ones:
- Flips are involutive. This fact follows immediately from the fact that a quadrilateral only has
2 diagonals.
- Any two triangulations can be obtained from each other by a sequence of flips. This is true even in the case of ideal triangulations of a bordered surface with marked points (Proposition 3.8 of Fomin-Shapiro-Thurston).
- Something that is not really relevant for our purposes, but certainly interesting is that if we label the vertices of the $n$-gon by $[n]$ (shorthand for the first positive $n$ integers) clockwise, then there is a natural association of the edges in the triangulation and Plucker coordinates. This gets into interesting discussions about total positivity of the Grassmannian $\text{Gr}_{2,n}(\CC)$. This relationship is relevant to flips because one can use the three-term Grassmann-Plucker relations to express the flip as a rational expression in the Plucker coordinates with no negative terms (and this is where the positivity part enters the picture). This can be read about more in the book Introduction to Cluster Algebras. Chapters 1-3 by Fomin, Williams, and Zelevinsky.
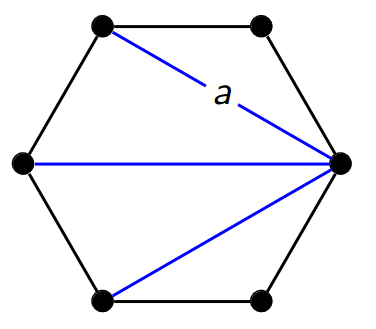
From here, we start introducing quivers. Suppose we start off with the triangulation again.

Then to each edge in the triangulation, we associate a vertex. We then add $3$-cycles oriented in the clockwise direction within each face via the associated vertices. This gives us the following:
What gets interesting is to observe the effect on the quiver when we do a flip of a diagonal:
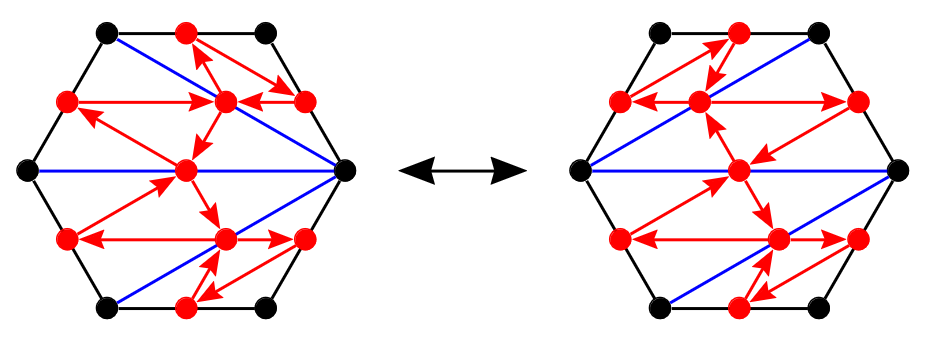
An observation that we can make is to notice that the effect of the flip on the quiver is contained entirely in the top half of the hexagon. In other words, the effect is local.
The goal of quiver mutation is to come up with a generalization of the effect flips have on quivers arising from triangulations. That is, we define an algorithm that generalizes flips by allowing for quivers that do not necessarily arise form triangulations of an $n$-gon. This motivates the following definition
[definition] A cluster quiver is a quiver without loops or $2$-cycles. [/definition]
And thus, we can define quiver mutation:
[definition] The mutation of cluster quiver $Q$ at vertex $x$ is a new quiver $\mu_x(Q)$ with same vertex set obtained as follows:
- For each path $w \to x \to y$, add a new arrow $w \to y$
- Reverse each of the arrows incident to $x$
- Remove any pairs of arrows forming a $2$-cycle and repeat until no more $2$-cycles exist in $Q$ [/definition]
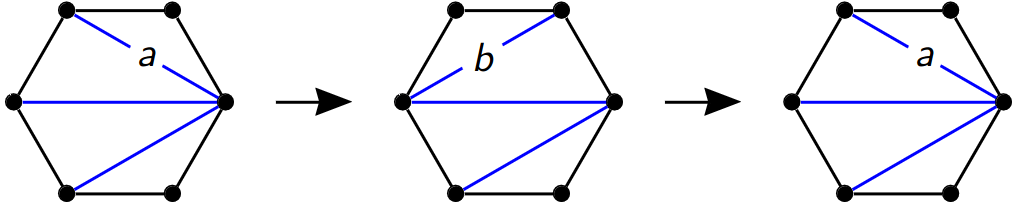
So at this point, we have been claiming that flips are generalized by quiver mutations. We can check that this claim holds for a quick example:
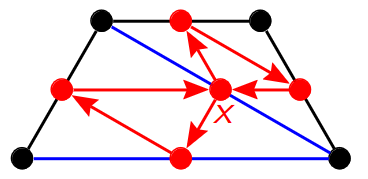
This was obtained by taking the earlier triangulation with the diagonal labeled $a$ (and its quiver) and only looking at the top half. We look at the top half only because the way quiver mutation is defined makes it a local transformation. In any case, the first step of quiver mutation gives
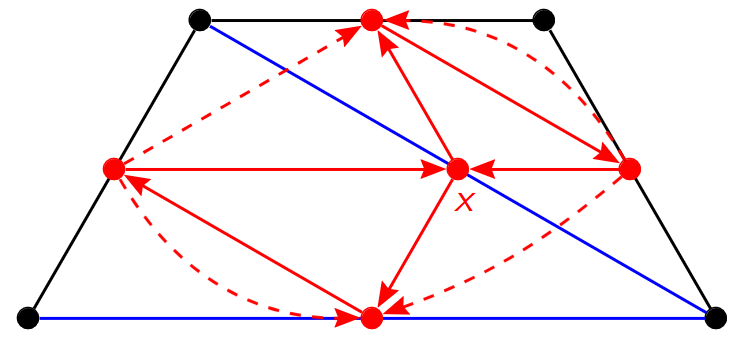
The second step of quiver mutation gives
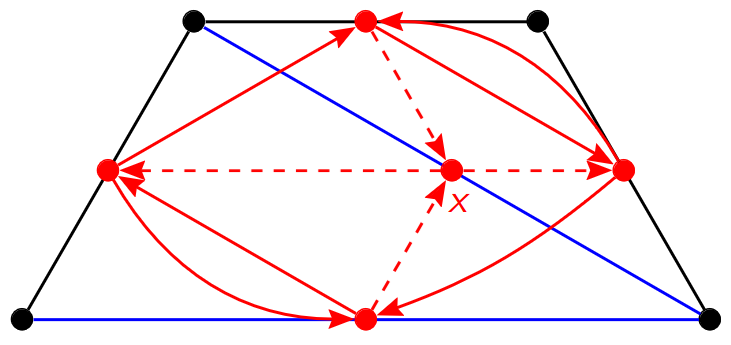
The third step of quiver mutation gives
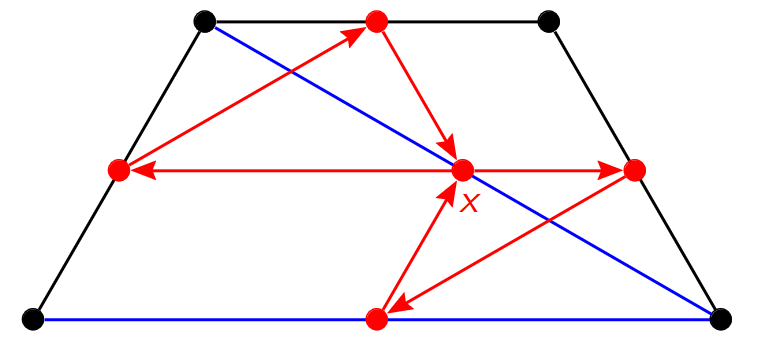
At this point, it might not be obvious as to what we are looking at. The connection becomes clear, however, once we update the triangulation (by flipping the diagonal) and then slide the quiver around (which is fine because we really consider it up to isotopy here).
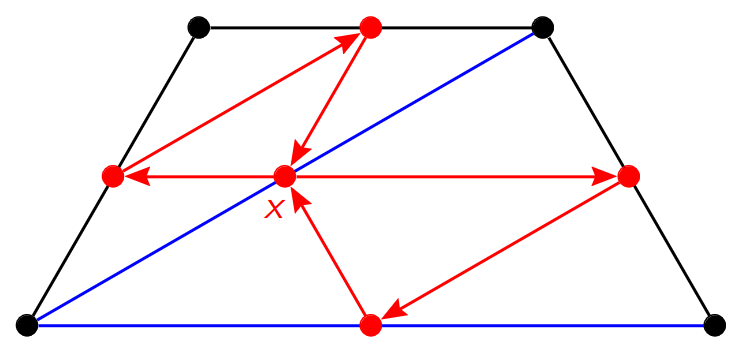
So for the case of triangulation quivers, we see that flips of the diagonal correspond to quiver mutations and vice versa. So indeed, the claim that quiver mutation generalizes flips of diagonals holds for this case. This claim is actually true even for ideal triangulations of bordered surfaces with marked points. This is Proposition 4.8 of Fomin-Shapiro-Thurston. If we were to look at this paper, though, it mentions matrix mutation rather than quiver mutation. These matrices, however, can still be thought of as quiver mutations! This is mentioned in Bernhard Keller’s paper on Cluster algebras, quiver representations, and triangulated categories.
Speaking of Bernhard Keller, there are some programs he developed that implement the quiver mutation algorithm. It is well-known and some papers even mention/use it for some calculations of mutation classes (i.e. the set of all possible quivers up to isomorphism obtained from a sequence of mutations). I would highly recommend spending some time playing with it.
In any case, quivers are well-studied by mathematicians (and physicist too, actually, quivers show up in theoretical physics!). So many properties of quivers and quiver mutation are well established. One easy property that I will mention is that quiver mutation is an involution: $\mu_x(\mu_x(Q)) = Q$. For other properties, consider looking at:
- Anna Felikson’s slides on Cluster algebras, quiver mutations and triangulated surfaces
- The second chapter of Introduction to Cluster Algebras. Chapters 1-3 by Fomin, Williams, and Zelevinsky
- If you look at this resource, you will immediately note that triangulation quivers are defined slightly differently using frozen vertices. This fixes a small sloppy detail I did not address earlier when I said that quiver mutation and flips are equivalent. They are not if the quiver is mutated at a $2$-valent vertex.
Comments